ベイズ線形回帰 #
本節では変分推論の枠組みで回帰問題を考えていきます。回帰問題は一般に$N$個の説明変数$\mathbf{x}$と目的変数$y$のセット、すなわち $$ \mathcal{D}={(\mathbf{x}_1, y_1),\cdots(\mathbf{x}_i, y_i)\cdots ,(\mathbf{x}_N, y_N)} $$ が与えられたとき、それぞれのサンプルに対して $$ y_i = f(\mathbf{w}, \mathbf{x}_i, \epsilon_i)\tag{1} $$ のように$y_i$を未知のパラメータ$\mathbf{w}$と説明変数$\mathbf{x}_i$と観測誤差$\epsilon_i$の関数で表されると仮定し、パラメータ$\mathbf{w}$をデータセット$\mathcal{D}$から推論するタスクになります。
$\mathbf{X}=\lbrace\mathbf{x}_1,\cdots, \mathbf{x}_N\rbrace$、$\mathbf{Y}=\lbrace y_1,\cdots, y_N\rbrace$とすると、$\mathbf{w}$、$\mathbf{X}$、$\mathbf{Y}$の同時確率は
$$ p(\mathbf{X},\mathbf{Y},\mathbf{w})=p(\mathbf{w})\prod_{i=1}^{N}p(y_i|\mathbf{x}_i,\mathbf{w})p(\mathbf{x}_i)\tag{2} $$ と書けることが分かります。ここで各サンプル間は独立であることをを仮定しており積の形で表せることに注意してください。この同時確率はグラフィカルモデルで表すと下図のように書けます。
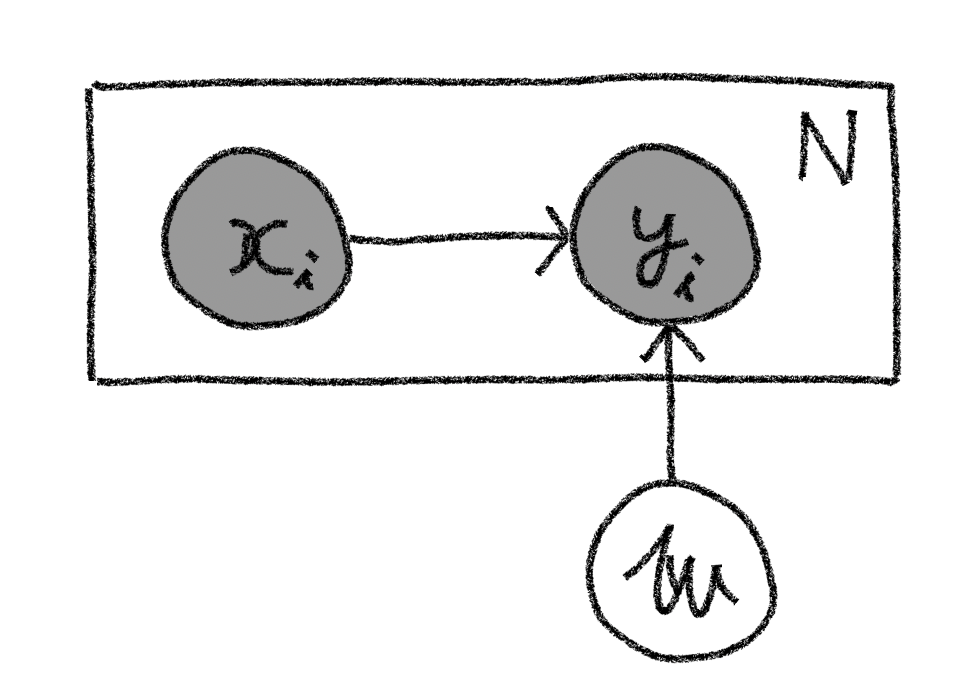
$\mathbf{X}$と$\mathbf{Y}$の組みが観測されたときの$\mathbf{w}$の事後分布は、事後確率の定義と(2)式から以下のように書けることが分かります。 $$ \begin{align} p(\mathbf{w}|\mathbf{X},\mathbf{Y})& =\frac{p(\mathbf{X},\mathbf{Y},\mathbf{w})}{p(\mathbf{X},\mathbf{Y})}\newline & =\frac{p(\mathbf{w})\prod_{i=1}^{N}p(y_i|\mathbf{x}_i,\mathbf{w})p(\mathbf{x}_i)}{p(\mathbf{Y}|\mathbf{X})p(\mathbf{X})}\newline & = \frac{p(\mathbf{w})\prod_{i=1}^{N}p(y_i|\mathbf{x}_i,\mathbf{w})}{p(\mathbf{Y}|\mathbf{X})}\tag{3} \end{align} $$ ここで2行目から3行目はデータサンプル間の独立性から$p(\mathbf{X})=\prod_{i}p(\mathbf{x}_i)$と書けることを利用しています。
このパラメータ$\mathbf{w}$の事後分布をデータから推定するタスクがベイズ回帰です。
■1次元線形回帰 #
まずは回帰の最も簡単な例として1次元線形回帰を考えていきましょう。この場合(1)式の具体的な関数型として $$ y_i=w_0 + w_1 x_i + \epsilon_i \tag{4} $$ と仮定することに相当します。ここで$\epsilon_i$を平均0、標準偏差$\sigma$のガウス分布に従う、つまり $$ \epsilon \sim \mathcal{N}(\epsilon|0, \sigma) \tag{5} $$ と仮定すると、(4)、(5)式をまとめることで $$ p(y_i|x_i,w_0, w_1, \sigma)=\mathcal{N}(y_i|w_0+w_1 x_i, \sigma)\tag{5} $$ と書けることが分かります。 ここで観測誤差の広がり度合いを示す$\sigma$も推定したいパラメータとすると(2)式は $$ p(\mathbf{X},\mathbf{Y},w_0,w_1,\sigma)=p(w_0)p(w_1)p(\sigma)\prod_{i=1}^N\mathcal{N}(y_i|w_0+w_1 x_i, \sigma)p(x_i)\tag{6} $$ という具体的な形に書くことができます。またこの同時確率をグラフィカルモデルで記述すれば以下の図のようになります。
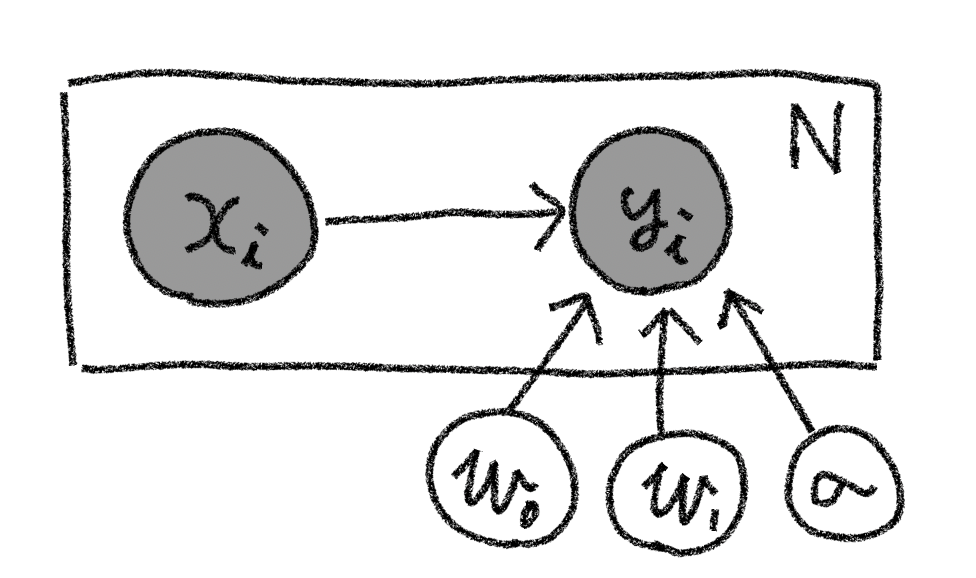
ここで未知のパラメータ$w_0$、$w_1$、$\sigma$(以降、これらを潜在変数と呼ぶ)の事後確率分布を求めるのが今回の一次元線形回帰のタスクになります。まずは (6)式の確率モデルをPyroを用いて記述し変分推定を行っていくところをみていきましょう。
なお以降では下記のコードを実行されている前提で話を進めていきます。
※プログラムコードの全体は Github上に公開しています。
import matplotlib.pyplot as plt
import numpy as np
import torch
from torch.distributions import constraints
import pyro
import pyro.distributions as dist
from pyro.infer import SVI, Trace_ELBO
from pyro.infer import Predictive
np.random.seed(1)
pyro.set_rng_seed(1)
また、下記のコードで生成されるToyデータセットを例に進めていきます。
def create_linear_data(w0=3.0, w1=2.0, sigma=5.0, size=20):
x = np.random.rand(size) * 10.0
y = w0 + w1 * x
y = y + np.random.normal(scale=sigma, size=x.shape[0])
return x, y
x, y = create_linear_data()
train = torch.tensor(np.array([x, y]).T, dtype=torch.float)
このコードで生成されるデータは(1)式において$w=2.0$、$b=3.0$とし、観測誤差が標準偏差5.0のガウス分布で発生するとしたデータになります。生成されたデータは以下のグラフのようになります。このToyデータセットをもとにベイズ線形回帰を行っていきましょう。
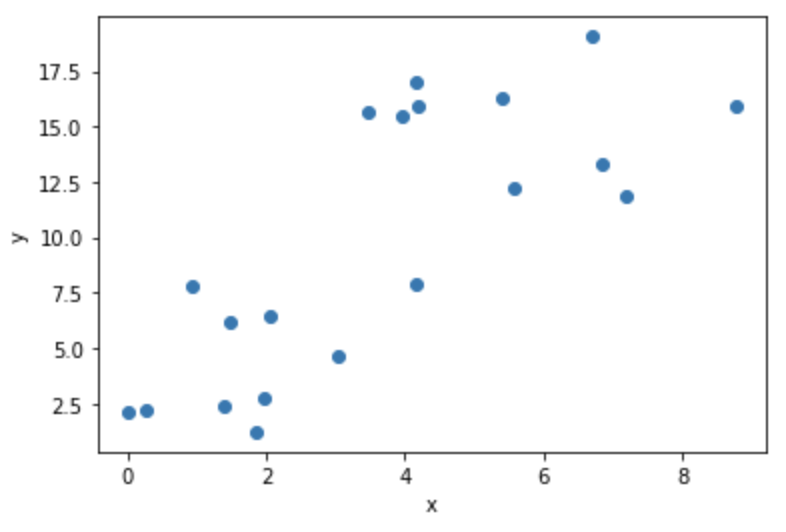
確率モデルの構築 #
(6)式の確率モデルをPyroを用いて関数として定義します。
def model(x, y):
w0 = pyro.sample("w0", dist.Normal(0., 10.))
w1 = pyro.sample("w1", dist.Normal(0., 10.))
sigma = pyro.sample("sigma", dist.Uniform(0., 10.))
mean = w0 + w1 * x
with pyro.plate("data", len(x)):
pyro.sample("obs", dist.Normal(mean, sigma), obs=y)
ここで、w0とw1の事前確率分布は平均0で標準偏差10の正規分布、sigmaは0~10の値をとる一様分布としていることになります。
変分関数を指定 #
次に変分関数を定義します。こちらも Pyroでの変分推論の節と同様、guide関数で実装することになります。今回は以下のコードのように実装します。
def guide(x, y):
w0_loc = pyro.param('w0_loc', torch.tensor(0.))
w0_scale = pyro.param('w0_scale', torch.tensor(1.), constraint=constraints.positive)
w1_loc = pyro.param('w1_loc', torch.tensor(0.0))
w1_scale = pyro.param('w1_scale', torch.tensor(1.0), constraint=constraints.positive)
sigma_loc = pyro.param('sigma_loc', torch.tensor(1.), constraint=constraints.positive)
sigma_scale = pyro.param('sigma_scale', torch.tensor(0.5), constraint=constraints.positive)
w0 = pyro.sample("w0", dist.Normal(w0_loc, w0_scale))
w1 = pyro.sample("w1", dist.Normal(w1_loc, w1_scale))
sigma = pyro.sample("sigma", dist.Normal(sigma_loc, sigma_scale))
上記コードでは、今回推定したいパラメータ(潜在変数)$w_0$、$w_1$、$\sigma$の事後確率分布をそれぞれ正規分布と仮定していることになります。正規分布を特徴付けるパラメータは平均locと標準偏差scaleのため、以降の推論パートではELBO最大にするように潜在変数毎のこれら2つのパラメータを最適化することになります。そのため潜在変数それぞれの平均と標準偏差をpyro.paramを用いて定義することにより、これらが最適化対象の変数であるということをPyroに伝えます。また標準偏差は正の値をとるためconstraint=constraints.positiveとして正値のみをとるように制約条件を課していることに注意してください。また、繰り返しですがguide関数の引数はmodel関数と同一でないといけないことに注意してください。
推論 #
確率モデルと変分関数を定義したら、あとは推論を行っていきます。こちらも 変分推論を試すと同様であることがわかるでしょう。
optimizer = pyro.optim.Adam({"lr": .1})
svi = SVI(model, guide, optimizer, loss=Trace_ELBO())
x, y = train[:, 0], train[:, 1]
pyro.clear_param_store()
num_iters = 5000
iter_nums = []
losses = []
for i in range(num_iters):
loss = svi.step(x, y)
iter_nums.append(i + 1)
losses.append(loss)
if i % (num_iters / 10) == 0:
print("Elbo loss: {}".format(loss))
plt.plot(iter_nums, losses)
plt.xscale("log")
plt.show()
## Output
# Elbo loss: 929.2532387375832
# Elbo loss: 62.93969136476517
# Elbo loss: 63.404844522476196
# Elbo loss: 64.26783436536789
# Elbo loss: 64.90034347772598
# Elbo loss: 63.357214510440826
# Elbo loss: 62.72878021001816
# Elbo loss: 73.45997166633606
# Elbo loss: 63.51271438598633
# Elbo loss: 63.471219420433044
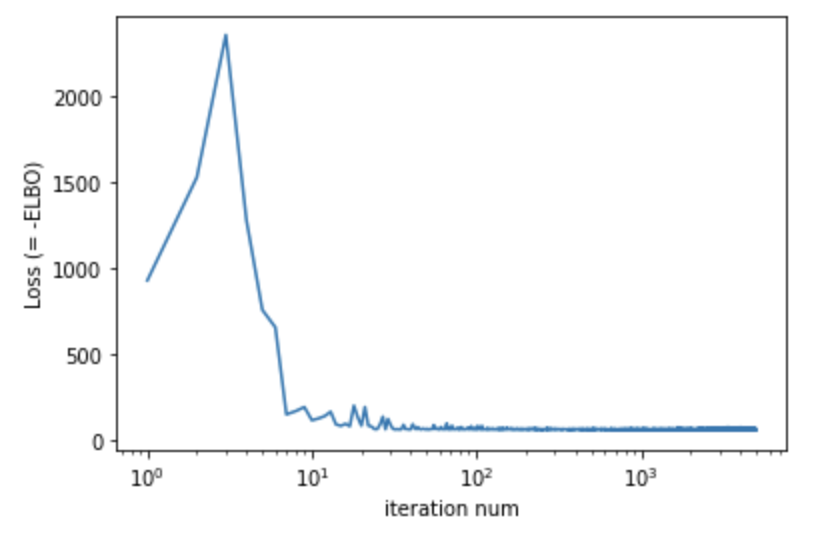
学習モデルの確認 #
学習結果のパラメータの内容はpyro.get_param_store()から参照可能です。最適化されたパラメータを出力してみましょう。
for name, value in pyro.get_param_store().items():
print("{} = {:.3f}".format(name, pyro.param(name).item()))
### Output
# w0_loc = 2.959
# w0_scale = 0.840
# w1_loc = 1.842
# w1_scale = 0.182
# sigma_loc = 4.156
# sigma_scale = 0.614
これらのパラメータから潜在変数の事後確率分布をプロットしてみましょう。
x_range = np.arange(0.0, 6.0, 0.01)
latent_vars = ["w0", "w1", "sigma"]
for latent_var in latent_vars:
param_loc = latent_var + "_loc"
param_scale = latent_var + "_scale"
inferred_dist = dist.Normal(pyro.param(param_loc).item(), pyro.param(param_scale).item())
inferred_y = [inferred_dist.log_prob(torch.tensor([x])).exp() for x in x_range]
plt.plot(x_range, inferred_y)
plt.show()

学習の結果、潜在変数の事後分布はトイデータを作成した正解の値に近いところを中心にそれぞれ分布しているのが見て取れます。 また、潜在変数の事後分布の平均値で回帰直線を引いてみると以下のようになります。
plt.scatter(x, y)
x_test = np.arange(0, 10, 0.1)
w0_loc = pyro.param("w0_loc").item()
w1_loc = pyro.param("w1_loc").item()
y_test = w0_loc + w1_loc * x_test
plt.plot(x_test, y_test)
plt.show()
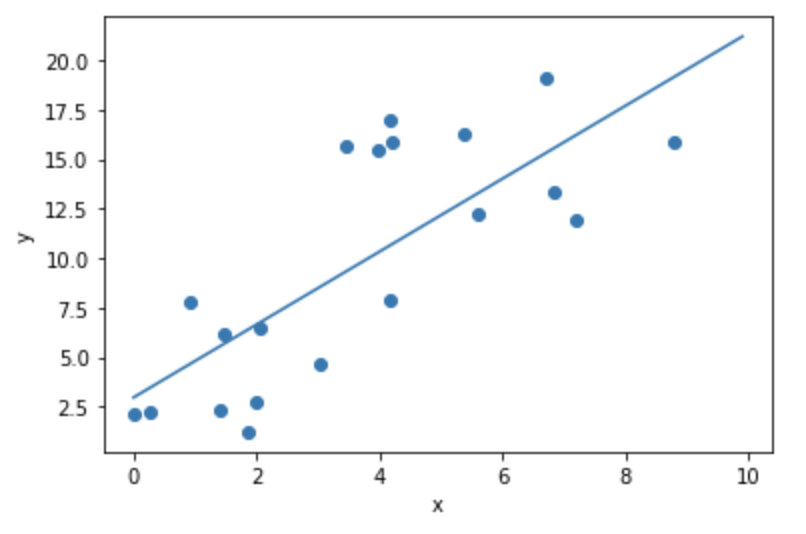
サンプルに沿った回帰直線が引けて学習が正常に動いているのが見て取れます。
Hint
今回は変分関数としてガウス分布を指定しているため、事後分布の平均値はすなわち事後分布の最大点と等しくなります。つまり上の図はMAP推定をした場合の回帰直線を意味していることになります。
また学習した潜在変数の事後分布からサンプリングを行うことも可能です。サンプリングには下記のコードのようにpyro.infer.Predictiveのクラスを利用すると便利です。
X_range = torch.tensor(np.linspace(0, 10, 50))
predictive = Predictive(model=model, guide=guide, num_samples=1000, return_sites=["w0", "w1", "obs"])
predict_samples = predictive.get_samples(X_range, None)
このコードではX_range変数に格納された$x=0\sim 10$の範囲の50の点それぞれに対して、指定されたmodelとguideの関数に従って1000回サンプリングを行うことをしています。またサンプリングされる量はreturn_sitesで指定された確率変数がサンプリングされます。
さて、これを利用して回帰直線の90%信頼区間をプロットしてみます。
sampled_vals = predict_samples["w0"] + predict_samples["w1"] * X_range
mean_vals = sampled_vals.mean(0)
percent05_vals = sampled_vals.kthvalue(int(sampled_vals.shape[0] * 0.05), dim=0)[0]
percent95_vals = sampled_vals.kthvalue(int(sampled_vals.shape[0] * 0.95), dim=0)[0]
plt.scatter(x, y)
plt.plot(X_range, mean_vals, color='r')
plt.fill_between(X_range, percent05_vals, percent95_vals, color='r', alpha=0.2)
2行目でサンプリングされた$w_0$,$w_1$をもとに目的変数$y$を計算しています。4と5行目で、これらサンプリングされた点から5%,95%パーセンタイル値を取得。結果をプロットしています。
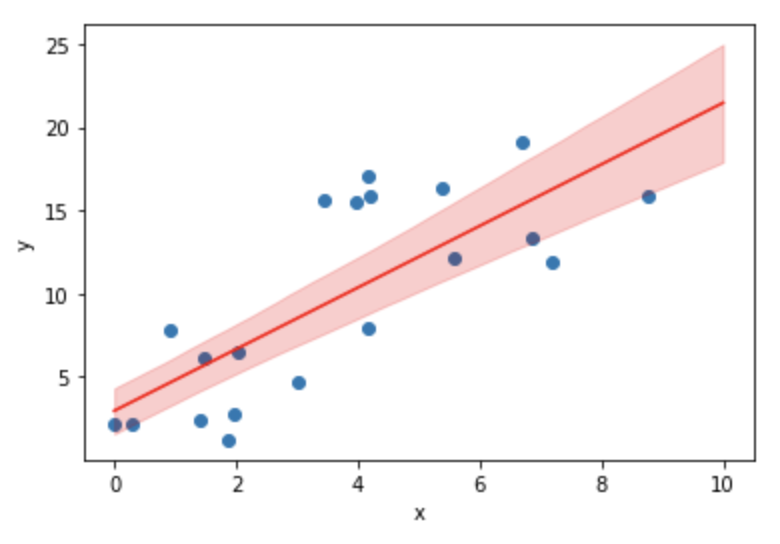
90%信頼区間の領域中に多くの観測値が入っていないのに注意してください。これは上図が回帰線の信頼区間をプロットしており観測誤差を考慮にいれていないことに起因します。
上図のような信頼区間の回帰線に観測誤差$\sigma$が加わる「観測値」はどの範囲に広がるのかを調べてみます。ここでは「観測値」の90%信頼区間をプロットしてみましょう。model関数内で観測誤差$\sigma$を含んだ観測値はobs変数として定義したのを思い出すと、obs変数のサンプリング値を利用すると目的の信頼区間が得られることが分かります。上記の回帰直線の信頼区間をプロットしたのと同様に以下のコードで観測値90%信頼区間がプロットできます。
# 観測誤差も考慮したの90%信頼区間をプロット
sampled_vals = predict_samples["obs"]
mean_vals = sampled_vals.mean(0)
percent05_vals = sampled_vals.kthvalue(int(sampled_vals.shape[0] * 0.05), dim=0)[0]
percent95_vals = sampled_vals.kthvalue(int(sampled_vals.shape[0] * 0.95), dim=0)[0]
plt.scatter(x, y)
plt.plot(X_range, mean_vals, color='g')
plt.fill_between(X_range, percent05_vals, percent95_vals, color='g', alpha=0.2)
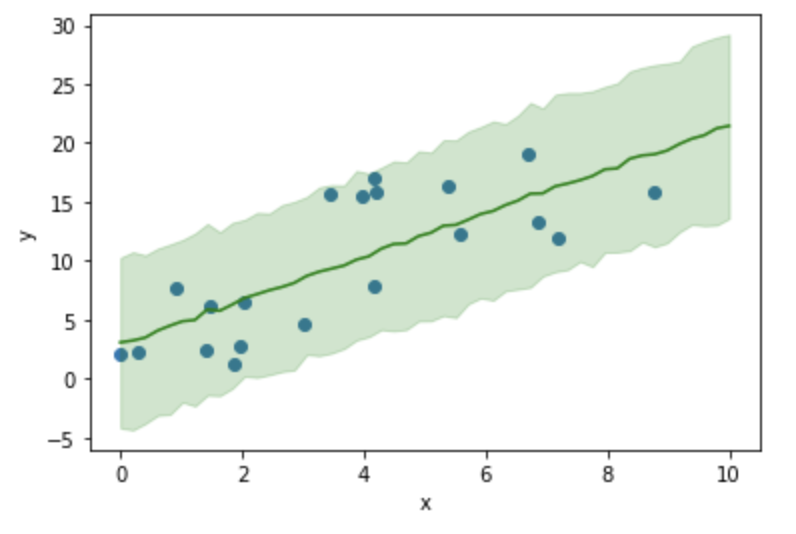
多くの観測値が90%信頼区間に入っており、今回ベイズ学習した回帰モデルでデータセットが上手く表現出来ていることが見て取れます。このように学習したモデルが実際の観測値を再現できるかを確認することはモデルの有効性を評価・確認する上で重要です。